In questo articolo andremo a vedere nel dettaglio cos’è e quando va utilizzato il test non parametrico di Mann-Whitney.
In modo molto rapido vedremo cosa sono i test non parametrici e come si differenziano dai test parametrici, per poi vedere più a fondo in cosa consiste il test U di Mann-Whitney e come effettuarlo su SPSS, Stata e R.
Nel caso un cui dovessi avere ancora dei dubbi o dovessi aver bisogno di una consulenza da parte di un esperto contattaci
Cosa sono i test non parametrici
I test più comunemente usati per effettuare analisi inferenziali sono costituiti da tecniche parametriche. Con statistica parametrica si intendono quelle tecniche statistiche basate su assunzioni circa la distribuzione della popolazione da cui viene selezionato il campione. Per esempio, per eseguire un t-test per la verifica di ipotesi su una media, è necessario assumere che i dati campionari provengano da una popolazione normalmente distribuita.
Le tecniche non parametriche sono utili quando ci accorgiamo che la distribuzione è ben lungi dalla normalità e/o il numero di osservazioni è molto scarso e non ci consente di utilizzare il teorema limite centrale.
Le tecniche statistiche non parametriche richiedono meno ipotesi sulla distribuzione e sui parametri della popolazione da cui è estratto il campione.
Talvolta queste tecniche sono chiamate distribution free perché possono essere usate qualunque sia la forma della distribuzione della variabile di interesse.
Nel caso di verifica di ipotesi, questa potrà sempre riguardare un parametro della popolazione ma il modello di riferimento sarà non parametrico.
Inoltre, queste tecniche sono adatte anche quando la variabile di interesse è di tipo Ordinale (ad esempio una Likert) o Nominale.
Cos’è il test U di Mann Whitney
L’ipotesi nulla nel test di Mann-Whitney (MW) è quella che i due campioni siano tratti da una popolazione singola, e che dunque per questa ragione le loro distribuzioni di probabilità siano eguali.
L’ipotesi alternativa è che uno dei campioni sia più grande in maniera stocastica. Questo richiede che i due campioni siano statisticamente indipendenti e che le osservazioni siano almeno ordinali, o quantitative continue o discrete.
Gli assunti del test di MW sono:
- I due campioni sotto studio da parte del test sono reciprocamente indipendenti e le osservazioni all’interno di ogni campione sono indipendenti;
- Le osservazioni sono confrontabili (ad.es., per qualsiasi due osservazioni, uno può stabilire se esse siano eguali oppure se al contrario, quale delle due sia maggiore).
Questo test viene utilizzato per effettuare confronti sulle mediane di due sottogruppi di osservazioni, per una variabile di tipo Ordinale o Scala.
Il test di Mann-Whitney costituisce quindi la controparte non parametrica del t-test a campioni indipendenti.
Le ipotesi si possono riformulare anche in questo modo: la nulla è che le mediane dei due sottogruppi (di X1e X2) non siano significativamente differenti, mentre l’alternativa è che vi sia una differenza statisticamente significativa.
Le formule per calcolare la statistica test sono le seguenti:
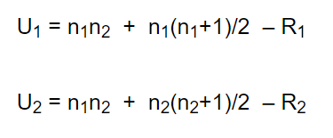
Dove n1 e n2 sono le numerosità campionarie, R1 e R2 la somma dei ranghi per il campione 1 e 2 rispettivamente.
Una volta calcolate entrambe le statistiche test si sceglierà la più piccola per decidere se rifiutare o accettare l’ipotesi nulla del test.
Di seguito sono riportati alcuni esempi di quando si potrebbe usare il test U di Mann-Whitney:
- Si vogliono confrontare i salari di cinque laureati da un’università A con i salari di cinque laureati da un’università B. I salari non sono distribuiti normalmente.
- Si vuole indagare se la perdita di peso differisce tra due gruppi: 12 persone hanno usato la dieta A mentre 10 persone la dieta B. La perdita di peso non è normalmente distribuita.
- Si vuole indagare se il punteggio di 8 studenti della classe A differisce da quello di 7 studenti della classe B. Il punteggio non è distribuito normalmente.

Come si svolge il test di Mann-Whitney su SPSS, Stata e R
Adesso vedremo come effettuare il test di Mann-Whitney su SPSS, Stata e R.
Su SPSS, come per moltissime altre cose, si potrà effettuare il test grazie ai menù a tendina presenti; in particolare si dovrà cliccare sul menù “Analizza” e poi seguirei comandi presenti nella foto di seguito.
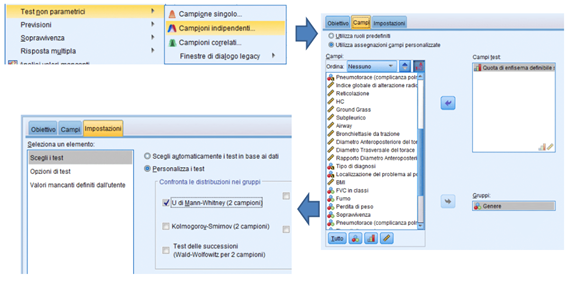
Su Stata e su R invece il test di Mann-Whitney potrà essere effettuato attraverso un comando:
- su Stata questo è ranksum var1, by var2
- su R è wilcox.test(var1, var2).
Per ulteriori informazioni o per una consulenza personalizzata, non esitare a contattarci!

Articolo a cura del Dott. Iacopo Moses





